工博士机器人技术有限公司是一家集研发、生产、销售、技术服务于一体的专注于自动化、智能化设备生产和机器人系统集成应用的科技型企业,与ABB、库卡KUKA、发那科FANUC、安川YASKAWA、欧地希OTC、川崎Kawasaki、遨博AUBO、现代HYUNDAI、电装DENSO、欧姆龙OMRON、爱普生EPSON等机器人公司签订了战略合作关系。
公司业务范围:
◆机器人本体及配套产品销售、机器人应用技术培训服务;
◆机器人在焊接、切割、搬运、激光技术、机床上下料、钣金折弯、锻造等领域的系统集成应用;
◆机器人变位机、导轨、防护工作房、焊接工装夹具等系统周边设备的设计和生产。
地址:上海市嘉定区南翔镇众仁路399号B座20楼2007室(王工:18616566200)
----------------------------------------------------------------------------------------------------------
目 录
几段协作6轴/7轴仿真动画:
3.1.1 逆运动学基本方法
一般而言串联式机械臂逆运动学有代数法和几何法。
代数法通用性强,但实时性差,广泛采用的是基于雅克比矩阵的伪逆法。
几何法实时性好,但是构型有一定的要求。即构型符合Pieper准则:机器人的三个相邻关节轴交于一点或三轴线平行。一般而言,构型一旦变化,几何法就得重新推导,但是当满足Pieper准则时,几何法的指导思想可以借鉴。
图3-1为6轴,7轴机器人常见的构型,其中至少有一组3个相邻的关节轴线交于一点。
图3-1 构型1:3个相邻轴线交于一点
图3-1(a)为绝大多数工业机械臂采用的构型,构型几何特定决定了后3轴交于一点,一般称该点为腕部点,可以将后3个关节坐标系的原点都放在腕部点上,末端位姿确定的情况下,腕部点位置确定(齐次矩阵变换法),随后以腕部点位置求解关节1,2,3角度,此过程采用几何法或者齐次矩阵中位置分量相等的代数方法,后综合末端姿态以及关节1,2,3角度,求解关节4,5,6的角度。
图3-1(b)为大多数七轴冗余协作机器人采用的构型,它有三组相邻3轴交于一点,那么关节轴1,2,3、关节轴3,4,5以及关节轴5,6,7的交点分别记作肩部,肘部和腕部,此时肩,肘,腕3点的位置将是重点关注对象,几何法逆解过程也由此展开,肩部,腕部以及关节4角度仅由末端位姿确定。肘部点位置需要一个冗余参数作为一个约束,以得到有限个逆解关节角度向量,同时也确定肘部位置。此时类比6轴工业机器人逆解过程,肘部点位置求解关节1,2,3角度,此过程采用几何法或者齐次矩阵中位置分量相等的代数方法,后综合末端姿态以及关节1,2,3角度,求解关节5,6,7的角度。详见3.3节iiwa几何逆运动学算法。
图3-2为6轴,7轴机器人中,常见的符合Pieper准则第二种情况构型的机器人,其中至少有一组3个相邻的关节轴线平行。
(a)相邻3轴线平行的6轴机器人 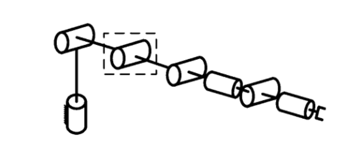 (b)有一组相邻3轴线平行的7轴机器人
(b)有一组相邻3轴线平行的7轴机器人
图3-2 构型2:3个相邻轴平行
图3-2(a)为优傲公司的UR系列机器人三维图,其关节2,3,4相互平行,那么关节2,3,4类似一个平面连杆机构,所在平面为与关节2,3,4轴线垂直的平面,关节坐标系4相对关节坐标系1的位置与姿态有特定的关系,这就是几何法的关键所在。基于此特点,可以将关节2,3,4的角度作为1个整体,关节1,5,6角度作为另一个整体求解,过程详见3.2节。
计UR5末端关节坐标系的齐次矩阵各项元素为下式:
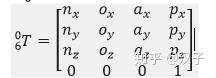 (3-1)
(3-1)
表 UR5机器人的改进DH参数
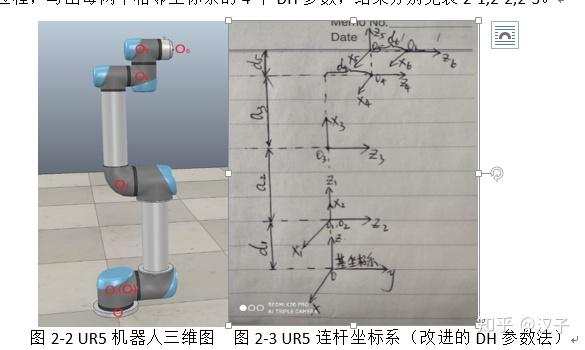

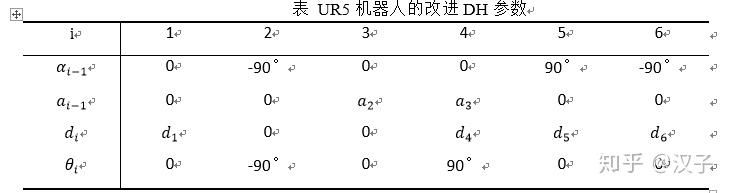

UR5作为一款全关节可360°旋转的新型人机协作机器人,其肩部、肘部与腕部的相邻关节2、3、4互相平行,满足机器人机构学中的 Pieper 准则,其运动学逆解具有封闭解。根据运动学正解的过程,那么坐标系O4相对坐标系O1的变换矩阵如下:
(3-2)
式中:
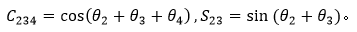
由上式知,关节2,3,4的转动,使得坐标系O4的原点相对坐标系O1原点位置向量的y轴分量恒为d4。并且相对旋转矩阵也表明,坐标系O4的x,y,z轴单位向量在坐标系O1y轴下的投影,分别恒定为0,0,1。这两点规律也正是关节2、3、4互相平行所造成的,同时我们观察图2-2的坐标系也能印证此规律:中第二行为定值[0,0,1,]。
正如同Pieper准则中三轴轴线交于一点的逆解算法,这三轴角度的求解往往作为一个整体。比如传统的6轴工业机器人,后三轴交于腕部一点的缘故,使得末端位姿决定了腕部点的位置,并且后三轴的转动不会影响腕部位置向量,那么前三个关节的运动就会决定腕部位置,随后腕部三个关节确定末端姿态,所以其运动学逆解(已知求)算法过程一般是:
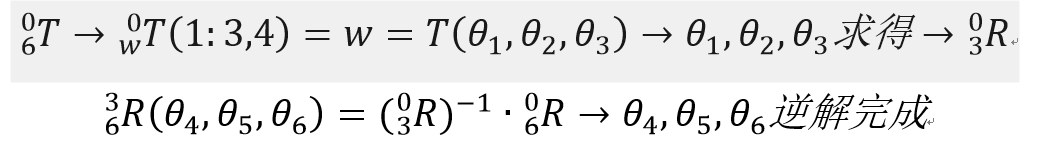
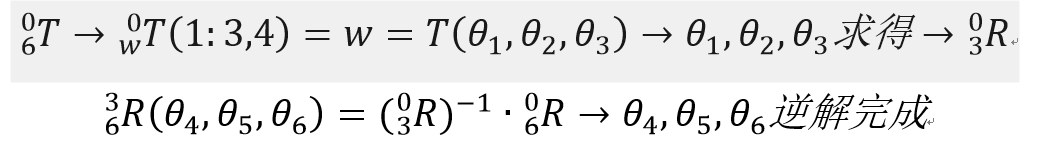
所以针对关节2、3、4平行的UR机器人,利用
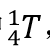
中第二行为定矩阵[0,0,1,],其逆运动学过程是先获得关节1、5和6的角度,再求解关节2、3和4的角度。
基于公式(3-2)中,以及运动学公式所以有:
(3-3)
式中:相关矩阵分别如下
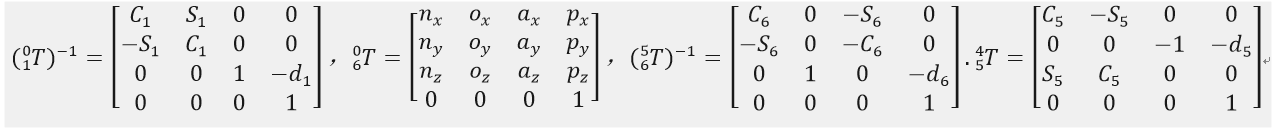
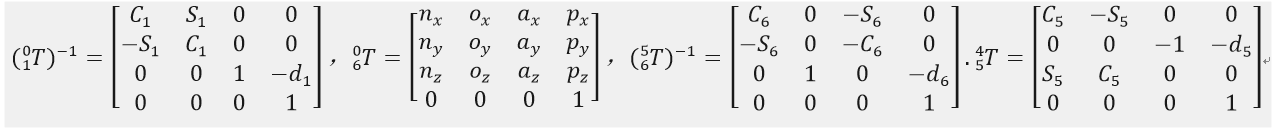
利用
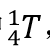
中第二行为定矩阵[0,0,1]我们重点关注公式(3-3)终矩阵中第二行的元素,所以方便得到下式(当然也可以进行符号运算得到完成的矩阵):
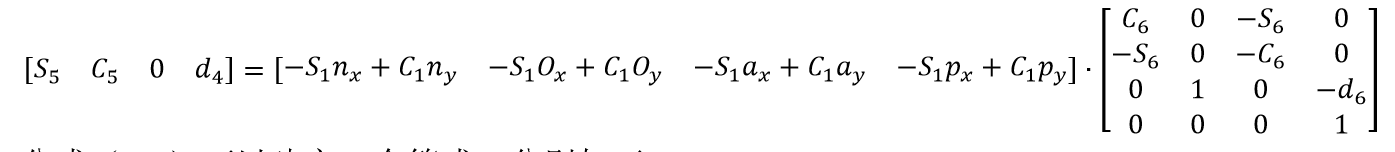
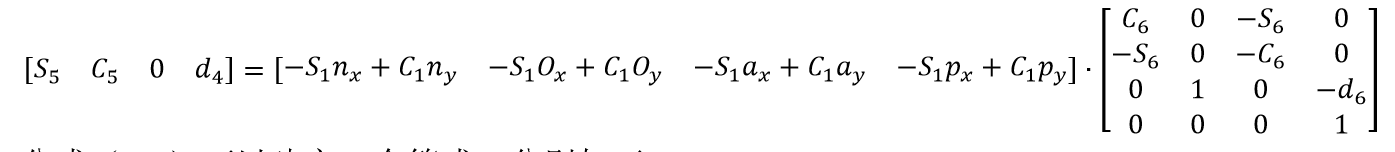 (3-4)
(3-4)
公式(3-4)可以建立4个等式,分别如下:
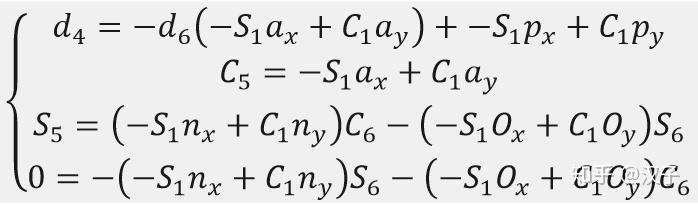
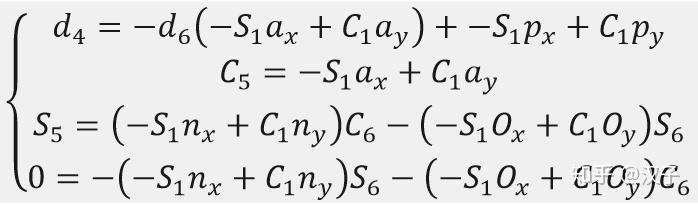 (3-5)
(3-5)
由公式(3-5)项可以获得关节1的逆解公式:
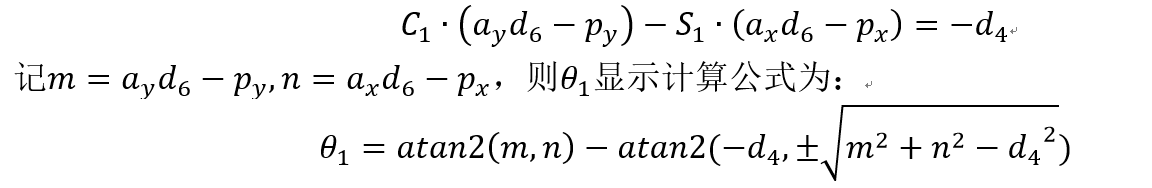
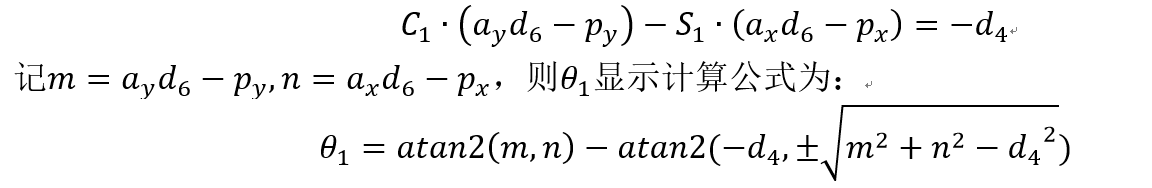 (3-6)
(3-6)
由公式(3-5)第二项,关节5的逆解公式为:
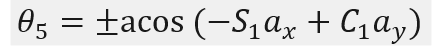
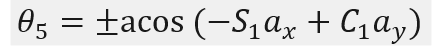 (3-7)
(3-7)
公式(3-5)第3项和第四项都可以得到关节6的逆解公式,但都有两个解,为此,联立二式,记,
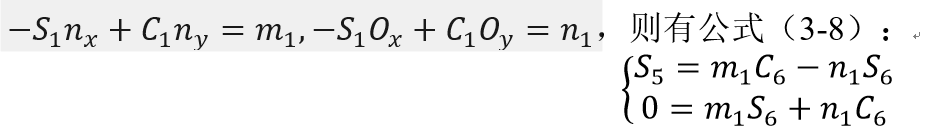
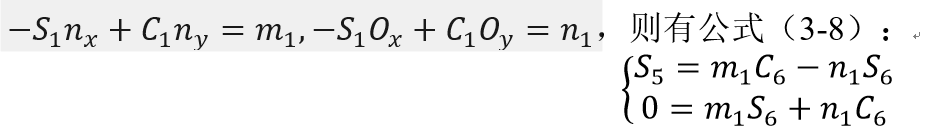 (3-8)
(3-8)
将公式(3-8)看成关于s6和c6的二元一次方程组,解得:
 (3-9)
(3-9)
所以的关节6的计算公式为:
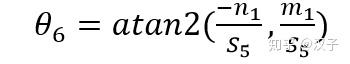 (3-10)
(3-10)
3.2.2 求解关节2,3,4的角度
现在关节1,5,6角度已经获得,再回到公式(3-3),继续在等式两端右乘
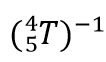
有:
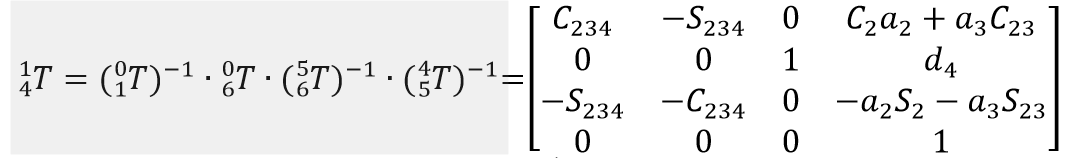
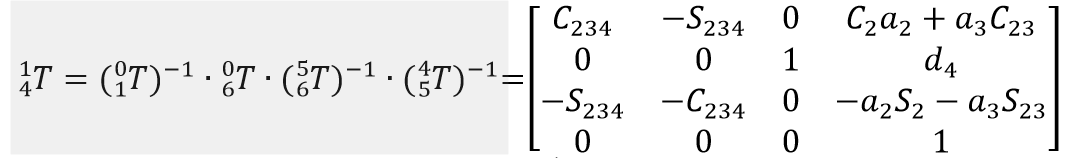 (3-11)
(3-11)
 (3-12)
(3-12)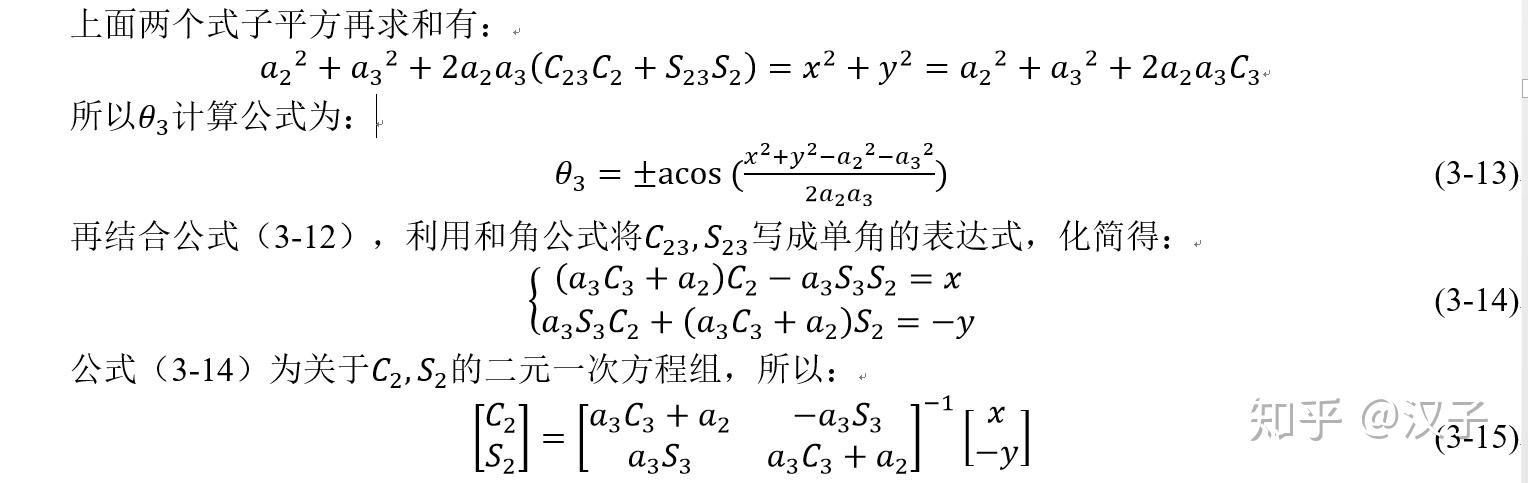
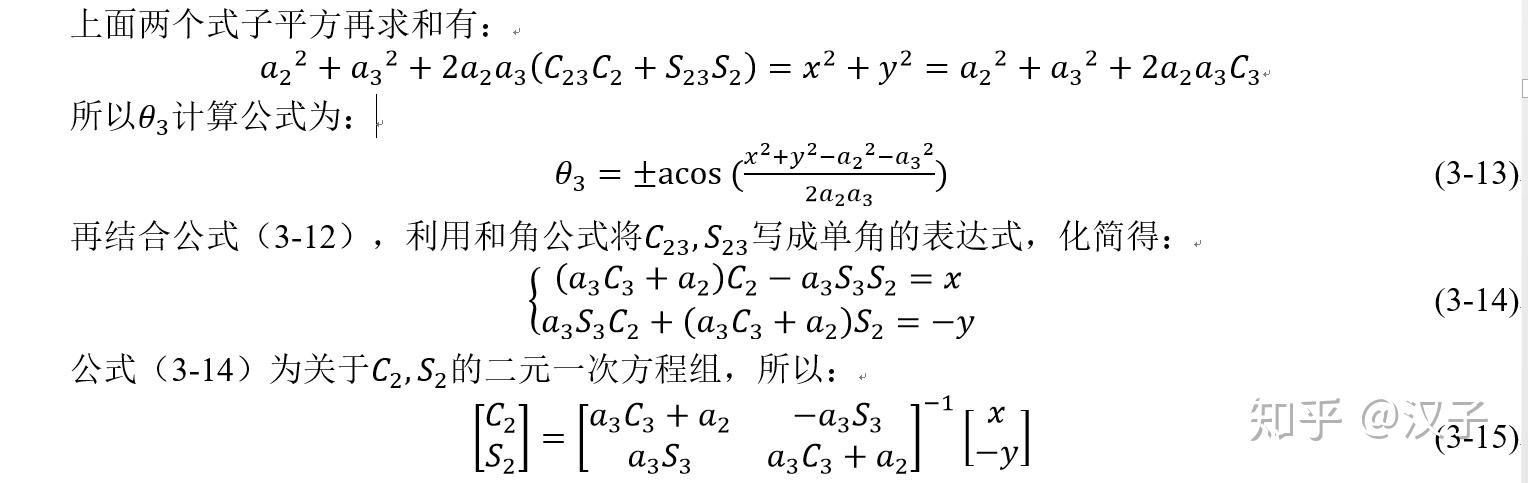
所以关节2的计算公式为:
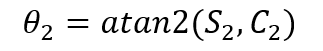 (3-16)
(3-16)
在公式(3-11)中:
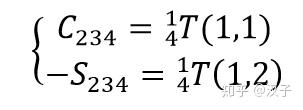 (3-17)
(3-17)
所以关节4的计算公式为:
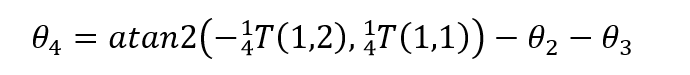 优傲机器人
优傲机器人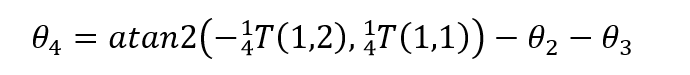 (3-18)
(3-18)
 优傲机器人
优傲机器人
将UR5逆运动学算法过程与逻辑,在simu
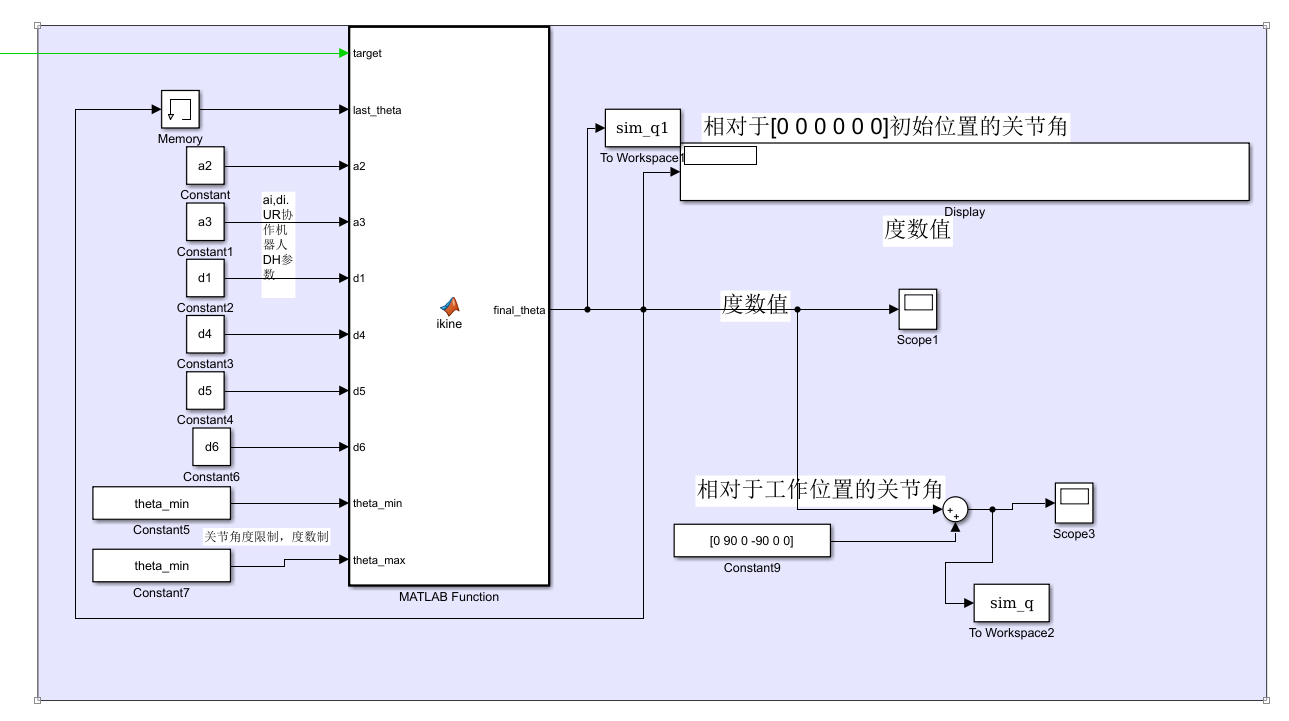
 UR机器人逆运动学模块,可以进行代码生成
UR机器人逆运动学模块,可以进行代码生成
当操纵空间维度 (m为末端夹持工具的自由度,多为6,分别为空间的3个移动和3个转动)小于关节空间维度 (n为有效运动关节的数量),机器人一定是运动学冗余的,这种冗余称优傲机器人为机器人本质冗余,与机器人的结构相关。比如,一个机器人的结构决定了机器人末端执行器只能在平面上移动和绕着平面法线的转动,但是该机器人有4个及以上的关节,那么该机器人一定是本质冗余的。末端执行器在空间中的运动多有6个自由度,如果机器人的结构允许末端执行器具有这6个自由度,但是有7个及以上的关节,那么机器人也一定是本质冗余的,具有性。
冗余自由度给运动学逆解带了很大的困难,但是机器人因此具有更多的灵活性,可以克服传统6轴串联机器人避障能力差的缺点,在保证末端执行器的位姿下,可以有连续的多解性。7关节的7轴协作机器人主要有两种构型,见图3-4,主要由位置构型和姿态构型组合而成,位置构型和姿态构型直接相连就是目前广泛应用于工业的传统6轴机器人。图3-4(b)和图3-4(c)两种构型机械臂的逆运动学均有封闭形式解,其中(b)代表的7自由度构型1为大量7轴机器人实际采用的构型,例如库卡公司iiwa,ABB公司YuMi,安川电机公司SDA,国内新松公司的7轴协作机器人等。
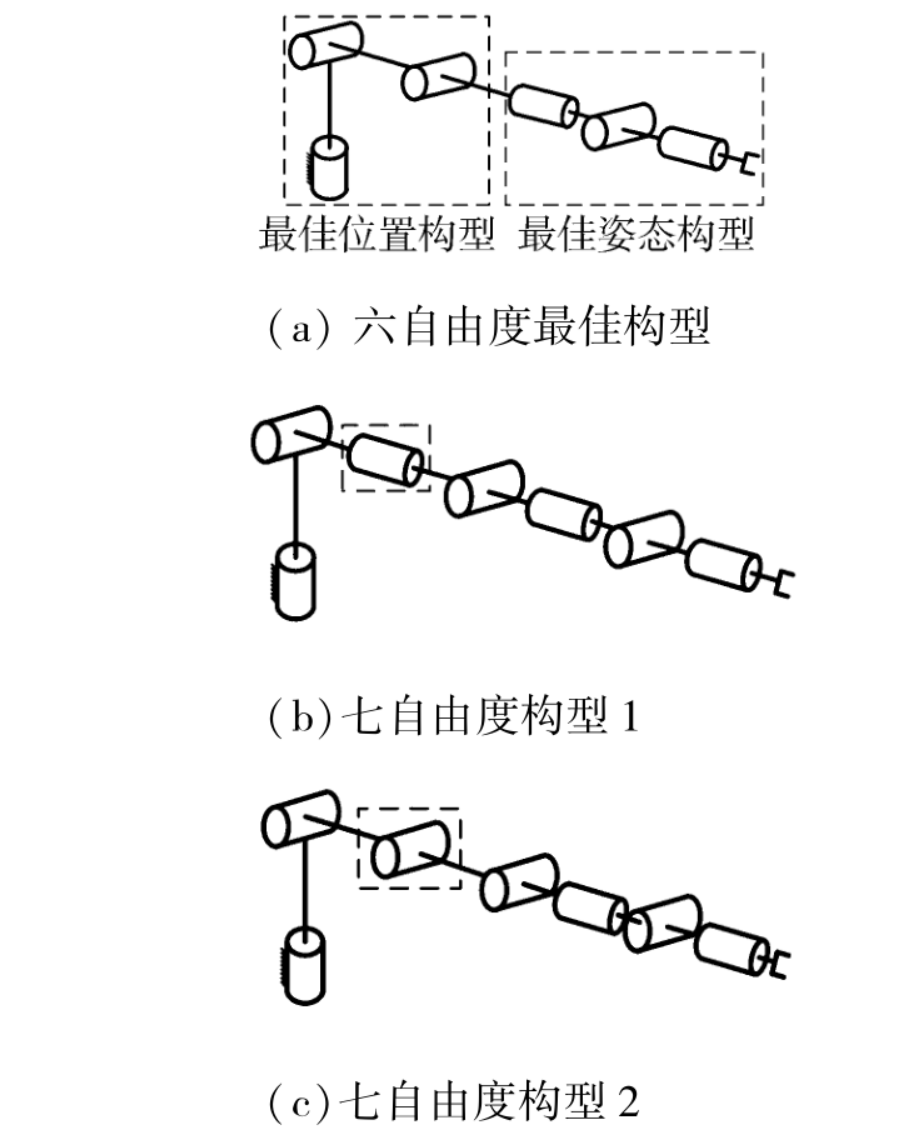
 图3-4 串联机械臂构型图
图3-4 串联机械臂构型图
在末端执行器位姿固定情况下,图3-4(优傲机器人b)构型1的肘部可以连续的运动,这可以调节机器人连杆在空间中的分布而不改变末端的位姿,这种特性使机器人具有很高的灵活性进行更安全可控的人机交互距离。本文以采用构型1的七自由度机器人为研究对象,选用iiwa_14_R820机器人的构型和尺寸参数,逆运动学算法直接适用于关节4无偏置的构型,该构型关节4轴线垂直相交于关节3,5的轴线交点处。
构型1关节4偏置的情况主要有两类,1类为安川电机的SDA5,见图3-5,关节3,5轴线依然共面相交,但关节4依然垂直于关节3和关节5所在的平面,即关节4垂直于纸面向里,但关节4轴线在的投影有一个左上角的偏置,分量分别为a4、a3,下文逆运动学的‘臂形角’解决方法不变,但细节有诸多不同。
图3-5 安川电机SDA5构型图
构型1关节4偏置的主要第二类为图3-4(b)中,关节4,5,6,7作为一个整体,在关节1、3所确定平面的法向量方向平移了一个偏置距离,可以使得可以得到的位置工作空间更大。‘臂形角’方法获得运动学逆解的方法依然可行,但是会存在两个共面于的‘冗余圆周’。在空间平面内,两个冗余圆周圆心形成的线段作为机架,两个冗余周周半径所在线段作为2个连架杆,由偏置距离形成的线段作为连杆,此机架、2个连架杆和连杆形成一个由臂形角(0-2pi)决定的,在空间平面上的平行平面四连杆机构,如此,保证了‘臂形角’方法依然适用。
标准DH参数的坐标系变换公式为:
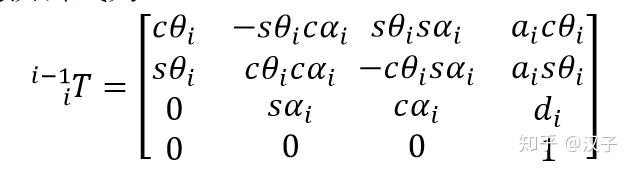
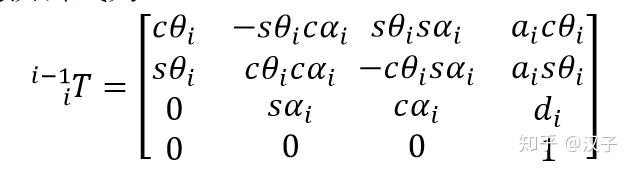 (3-3-1)
(3-3-1)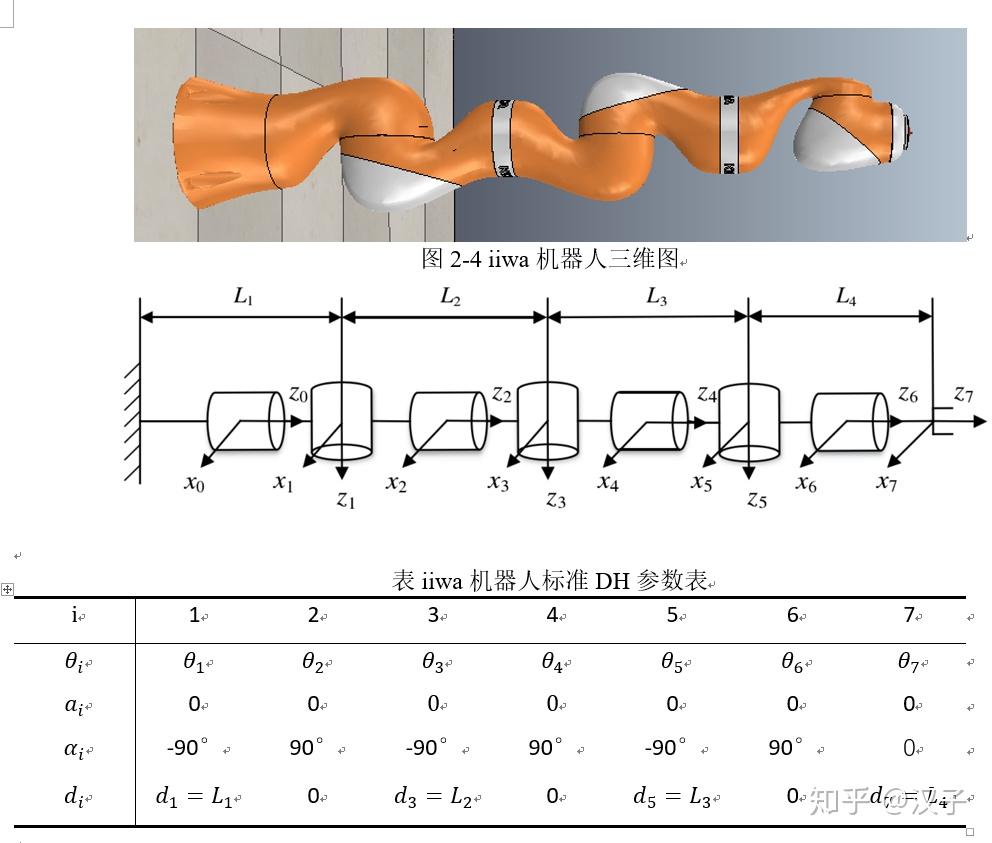

3.3.3关节4角度与臂形角
机器人关节角度为[0,0,0,90°,0,90°,0]时,7轴机器人的姿态如图3-6所示,肩部,肘部,腕部,大臂,小臂,该机械臂前三个关节轴线的旋转相当于一个以坐标系2原点为球心的球铰。同样,后三个关节的旋转也相当于一个球铰。这样机器人相当于人的手臂,前三个关节等效成肩关节S,第四个关节等效成肘关节E,后三个关节等效成腕关节W。当末端位姿给定时,因为后一个关节的转动对末端的位置没有影响,所以末端位置固定时,腕部位置也固定。同理个关节的转动也不改变肩关节的位置。
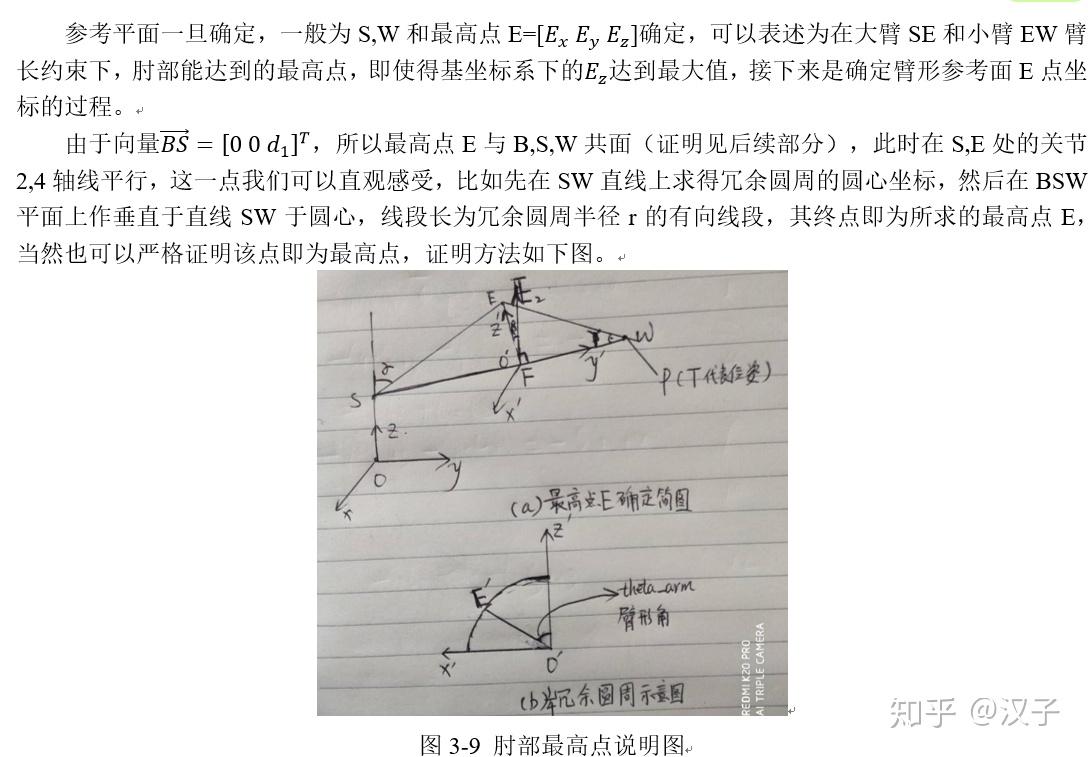
当末端位姿固定时,肘部E会绕着肩关节和腕关节连成的轴线旋转,如图3-7所示,这种肘部的旋转运动称为‘自运动’,肘部E点所在的圆周称为冗余圆周,其半径称为冗余半径,当确定一个参考平面,该平面由S,W和冗余圆周上点E(z轴分量)形成,当指定臂形角theta_arm时,theta_arm为引入的约束双臂(大臂和小臂)位置的参数,表示E绕着轴线SW旋转theta_arm度到达新的肘部E’点,每一个E’决定了大臂和小臂的位置,随后就可以解出关节4角度,以及关节1,2,3角度,后解算关节5,6,7角度。
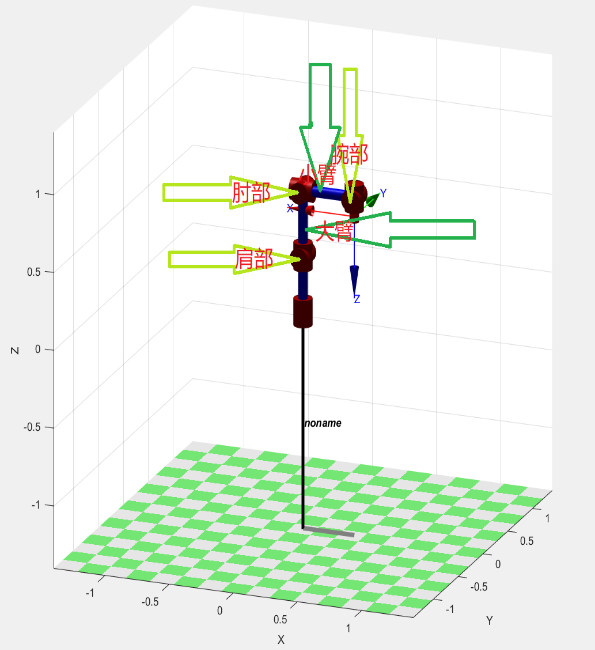
 图3-6 机器人肩,肘,腕示意图
图3-6 机器人肩,肘,腕示意图 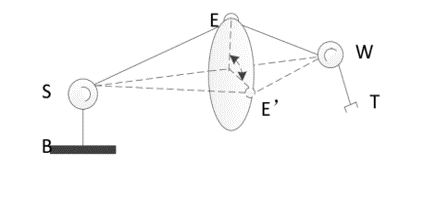
 图3-7 冗余圆周和臂形角示意图
图3-7 冗余圆周和臂形角示意图
结合机构构型,绕关节4轴线转动的效果,使得大臂和小臂形成一个夹角。所以关节4角度的求解可以转化为解三角形,如图3-8所示,关节4角度=q4(q4>0),且与内角SEW互补,但还有一种肘部E位置不变,E处关节4轴线由垂直于纸面向里(E处代表垂直于纸面向里)变成了垂直于纸面向外,变成-。例如在图3-6中,=[0,0,0,90°,0,90°,0],如果=-90°,那么前四关节向量为[0,0,-180°,-90°],依然可以使得肘部,大臂小臂的位置关系不变。所以的关节4的计算公式为:
(3-3-3)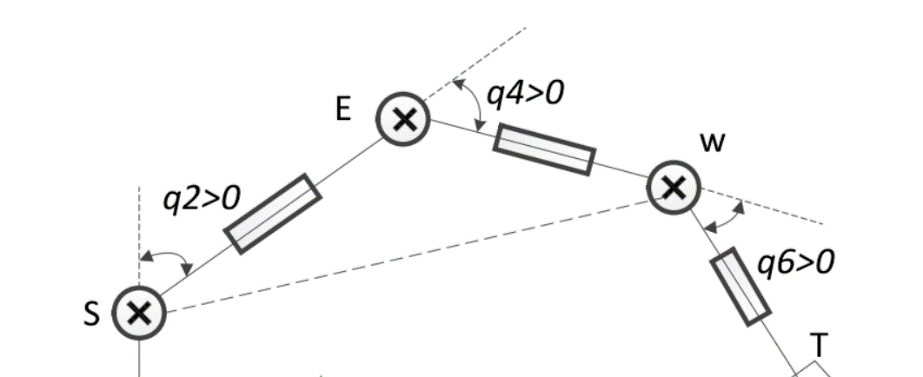
 图3-8 关节4角度求解示意图
图3-8 关节4角度求解示意图






旋转矩阵与关节1,2,3角度的求解








将iiwa逆运动学算法过程与逻辑,在simu
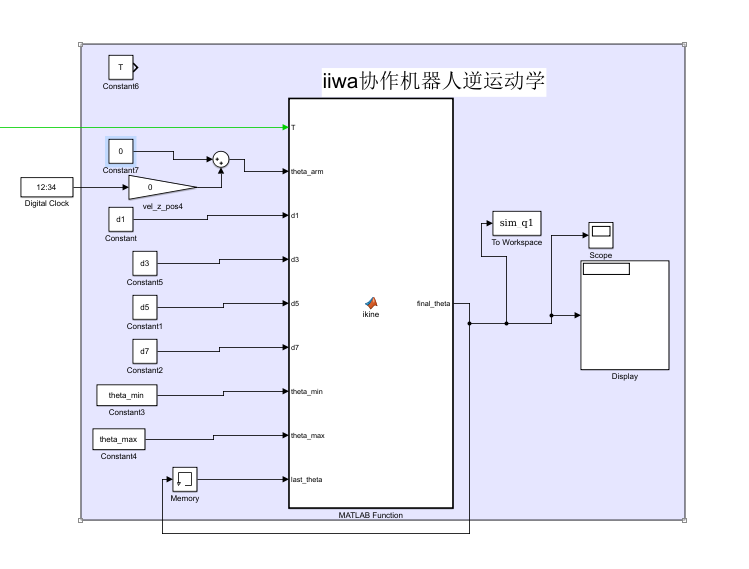
 图3-11 iiwa机器人逆运动学模块,可直接代码生成,效率优于数值迭代法
图3-11 iiwa机器人逆运动学模块,可直接代码生成,效率优于数值迭代法
主函数代码如下(暂略):



 图3-12,v-rep中iiwa走五角星轨迹,关节角度由matlab m函数计算给出
图3-12,v-rep中iiwa走五角星轨迹,关节角度由matlab m函数计算给出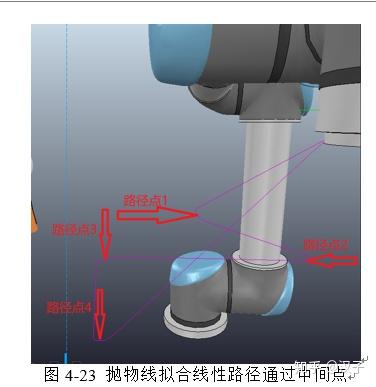
文章来源:https://zhuanlan.zhihu.com/p/326387013
更多咨询:优傲机器人




 产品:59
产品:59
 联系我们
联系我们
